2011年1月12日
エキゾチック球体、あるいは4次元空間はなぜクレイジーな場所なのか
エキゾチック球体、あるいは4次元空間はなぜクレイジーな場所なのか
リチャード・エルウェス
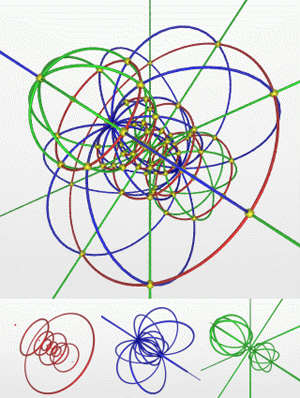 |
3次元の物体を2次元の平面に投影できるように、4次元の物体を3次元の空間に投影することができます。この画像は、4次元の超球を投影したものです。曲線は、超球の平行線(赤)、子午線(青)、いわゆる超子午線(緑)を投影したものである。
私たちが暮らす世界は、上下左右、前後という厳密な3次元の移動手段しかありません。しかし、科学者やSF作家は、もっと高い次元の空間について考えてきました。4次元、5次元の宇宙はどのようなものだろうか?3次元の立方体を切れば2次元の正方形になるように、3次元の世界は高次元の世界を切り開いたものに過ぎないのだろうか。
20世紀初頭のホラー作家H.P.ラヴクラフトによると、この高次元は実際に存在し、あらゆる種類の邪悪な生き物が住んでいるという。ラヴクラフトの神話では、これらの生物のうち最も恐ろしいのはヨグ=ソトースという名で呼ばれている。興味深いことに、ヨグ=ソトースはまれに人間界に現れると、「虹色の球体の集合体...その悪意ある暗示性において驚異的である」という形をとる。
20世紀初頭のホラー作家H.P.ラヴクラフトによると、この高次元は実際に存在し、あらゆる種類の邪悪な生き物が住んでいるという。ラヴクラフトの神話では、これらの生物のうち最も恐ろしいのはヨグ=ソトースという名で呼ばれている。興味深いことに、ヨグ=ソトースはまれに人間界に現れると、「虹色の球体の集合体...その悪意ある暗示性において驚異的である」という形をとる。
ラヴクラフトは数学にある程度の関心を持っており、実際、双曲線幾何学などのアイデアを用いて、彼の物語をより奇妙なものにした(Thomas HullがMath Horizonsで述べているように)。しかし、ヨグ=ソトースをこのような形で表現したことが、いかに幸運だったかを彼は知る由もないだろう。不思議な球体は、高次元世界への鍵であり、近年、その理解が大きく進んでいる。この50年間で、微分位相幾何学という学問が発展し、これらの場所がいかに異質であるかが明らかになった。
高次元と超球体
高次元と超球体
高次元は存在するのだろうか?この問いに対して、数学は驚くほど力強い答えを与えてくれる。2次元の平面が一対の軸を基準とした(5,6)のような座標の組で記述できるように、3次元空間は(5,6,3)のような数の組で記述できるのである。もちろん、この考え方は継続できる。数学者にとっての4次元空間は、(5,6,3,2)のような実数の4乗の集合と同定されるのである。この方法は、より高い次元にも適用できる。もちろん、このような次元が物理的に存在するかどうかという物理学者の質問には答えられない。しかし、数学的には、少なくとも、数を信じる限り、4次元空間も信じるしかないのである。
まあそれはいいとして、そんな空間はどうやって想像するのだろう?ヨグ=ソトースの隠れ家は実際にどうなっているのだろうか?私たちの脳は、3次元以上のものを見るようにはできていないので、この質問に答えるのはかなり難しい。しかし、ここでも数学的なテクニックが役に立つ。
その重要な例が球体です。地面のある場所を選んで、そこからちょうど1cm離れたところに印をつけると、半径1cmの円形ができあがります。同じことを3次元空間でやると、普通の球体や地球ができあがります。ところが、これとまったく同じことを4次元で行うと、最初の超球ができるのです。
これはどのようなものだろうか?さて、円を近くで見ると、それぞれの部分は普通の1次元の線のように見えます(だから、円は1球とも呼ばれるのです)。円と線の違いは、遠くから見ると、全体がカーブして自分自身とつながっていて、有限の長さしかないことです。同じように、通常の球体(つまり2球体)の各パッチは、2次元平面のパッチのように見える。ここでも、これらのパッチは、縁を残さず、有限の面積を持つように縫い合わされている。ここまでは予想通りだが、最初の超球(あるいは3球)でも全く同じことが言える。それぞれの領域は、見慣れた3次元空間と同じように見えるのである。私たちは、今、その中に住んでいるのかもしれない。しかし、低次元空間と同じように、全体は平らな3次元空間にはないカーブを描いており、辺がなく、有限の体積しかない形をしている。もちろん、ここで終わりではなく、次の超球(4球)は、すべての領域が4次元空間のように見えるようになり、さらにすべての次元で同じように見えるようになる。
幾何学から位相幾何学、微分位相幾何学へ
幾何学から位相幾何学、微分位相幾何学へ
幾何学と同様、トポロジーは図形を研究する数学の一分野である。基本的な疑問の1つは、2つの図形が本当に同じなのか、ということである。これには一意な答えがあるわけではなく、あなたが最も興味を持つ図形の側面に依存する。基本的なレベルでは、2つの図形が同じでありながら、異なる場所に位置している場合、ほとんどの目的では「同じ」であると数える。
トポロジーは、幾何学よりもはるかに広い範囲で「同じもの」という概念を持っている。ここでは、2つの図形は、一方が他方の形に引っ張られたり、伸ばされたり、ねじられたりすることができれば、「同じ」であると見なされるのである。つまり、トポロジストにとっては、三角形も台形も七角形もすべて同じ、ただの円である。一方、8の字は純粋に異なる形である。トポロジーの同一性の定義は、形を切ったり貼ったりすることには決して及ばないからである。つまり、切断が禁じられている8を円の形に引き込むことはできないし、小文字のiを接着することもできないのである。
角度や長さ、面積などに興味があるのなら、トポロジーの視点は間違っている。しかし、このレベルでも多くの重要なデータが保持されている。有名な例では、ロンドンの地下鉄の地図がある。例えば、ロンドンの地下鉄の地図は、トンネルの長さや正確なルートではなく、駅の並びや、異なる路線の交差の仕方などが重要です。これらはトポロジカルな現象であり、トポロジカルなモーフィングに耐えられる。そのため、ロンドンでは、地下鉄の正確なルートを記した詳細な地図ではなく、有名な簡略化した略図を使うことができるのだ。
トポロジーでは、ドーナツとマグカップは同じもので、一方は他方に変形することができます。
ドーナツ型のトーラスのように、穴が開いている図形もある。この穴は、トポロジカルなねじれや伸縮では取り除けない、本質的なものです。では、穴のない図形とはどのようなものだろうか?位相幾何学で最も有名な定理であるポアンカレ予想が、この問いにエレガントな答えを与えてくれる。立方体、ピラミッド、正十二面体など、さまざまな形が穴を持たないので、幾何学的な観点からは、これは正しくない。しかし、もちろんトポロジストにとっては、これらの刺激的な形はすべて球体にほかなりません。
ポアンカレ予想が本当に正しいことは、2002年以来わかっています(詳しくはPlusをご覧ください)。アンリ・ポアンカレは、3次元の球体に関する問題を提起しましたが、実はこれとまったく同じことが、より高い次元にも当てはまるのです。つまり、位相幾何学的に見ると、球体はどの次元でも美しくシンプルでユニークな物体なのだ。しかし、1956年、視点を少し変えるだけで、話が非常に複雑になることを示す最初の証拠が到着した。微分位相幾何学という新しい学問を通してアプローチすると、高次元空間の驚くべき秘密が明らかになり始めたのである。
ギャップ、キンク、コーナー
平板なトポロジーと微分トポロジーの違いは、非常に微妙なようで、驚くべき結果をもたらすことが判明している。それは、モーフィング処理中に許容される引っ張りや伸ばしの正確なタイプにかかっている。これは、「同じ」であるとみなされる形状に劇的な影響を与えます。
ジャンプしたり破れたりしない連続的な処理と、滑らかな処理に分けられる。滑らかであることは、単なる連続性よりもずっと強い条件である。円や球は滑らかな形だが、正方形や立方体は角が尖っているため滑らかとは言えない。しかし、これらの形は、縁に隙間や飛び出しがないため、すべて連続である。(不連続な線は2本に分かれている)また、どこまでも連続だが、どこまでも滑らかでないフラクタル模様もある。
同じように、私たちは、本当に滑らかなモーフィングと、連続的ではあるが非常にぎこちなく暴力的なモーフィングを区別することができる。しかし、この区別が本当に重要であるかどうかは、まったく明らかではない。トポロジーの観点からは同じ(専門的には同相)であっても、微分的な観点からは違う(差分同相ではない)、ということはあり得るのだろうか?言い換えれば、切らずに互いに変形できるけれども、変形が滑らかでなく、ぎこちなさやジャンプが必要な2つの図形があってもいいのだろうか?このようなことは、1次元、2次元、3次元では決して起こらないので、想像するのは確かに難しい。
これはジュリア集合と呼ばれるフラクタルである。その輪郭は連続的であるが、どこにも滑らかさはない。
エキゾチックな球体
1956年、7次元多様体の研究をしていたミルナー氏は、非常に奇妙な形状を発見した。一方では、穴がないので、球体のように見える。一方では、穴がないので球体のように見えるが、他方では、球体とは全く違う曲がり方をしている。当初ミルナーは、ポアンカレ予想の7次元版の反例を見つけたのだと思った。しかし、よく考えてみると、この新しい図形は、(ポアンカレが主張するように)球体に変形することができるのだが、驚くべきことに、それをスムーズに行うことができないのである。つまり、位相的には球面であっても、微分法では球面ではないのだ。
ミルナーは、最初のエキゾチック球体を発見し、さらに他の次元でもいくつかのエキゾチック球体を発見した。どの場合も、位相的には球面であったが、微分的には球面ではなかったのである。別の言い方をすれば、エキゾチック球体は、距離と曲率について通常の球体とは異なる概念を押し付ける方法である。
1次元、2次元、3次元では、エキゾチック球は存在せず、通常の球が存在するだけである。これは、トポロジカルな視点と微分的な視点が、これらの馴染み深い空間では発散しないためである。同様に、5次元と6次元には普通の球体があるだけだが、7次元になると突然28個になる。さらに高い次元では、1から任意の大きな数の間をちらちらと動き回る。
| Dimension | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Number of spheres | 1 | 1 | 1 | ? | 1 | 1 | 28 | 2 | 8 | 6 | 992 | 1 | 3 | 2 | 16256 | 2 | 16 | 16 |
現在でも最も謎に包まれているのは、4次元空間である。ここでは、エキゾチックな球体はまだ見つかっていない。同時に、存在し得ないことを証明した人もいない。4次元にエキゾチック球が存在しないという主張は、「滑らかなポアンカレ予想」として知られている。ここまで来て、まだよく分からないという人のためにはっきりさせておくと、 滑動ポアンカレ予想とポアンカレ予想とは別物である! 滑動ポアンカレ予想とポアンカレ予想にはいくつかの違いがある。ポアンカレ予想が証明されたのに対して、 滑動ポアンカレ予想は現在でも頑固なまでに未解決のままであるという違いがあるのです。
四次元の奇妙な世界
では、平滑ポアンカレ予想は正しいのだろうか?多くの数学者は、これはおそらく間違いであり、4次元のエキゾチック球が存在する可能性が高いという見解に傾いている。なぜなら、4次元空間はすでに非常に奇妙な場所であることが知られており、そこではさまざまな驚くべきことが起こるからである。その代表的なものが、1983年に発見された、全く新しいタイプの4次元の形状、すなわち、全く滑らかでない形状である。
先に述べたように、正方形は角が尖っているため、滑らかな形ではありません。しかし、平滑化することができる。つまり、円という滑らかな図形と位相的に同じである。しかし、1983年、サイモン・ドナルドソンは、4次元多様体の中に、滑らかでない新しいクラスを発見した。
この他にも、球体だけでなく、様々な異形が存在する。4次元空間(R4)そのものにも、さまざまな種類があることが分かってきた。通常の平坦な空間もありますが、それと並んでエキゾチックなR4があります。これらの空間は、位相的には通常の空間と同じであるが、差はない。驚くことに、1987年にクリフォード・タウベスが示したように、このような別の現実が実際には無限に存在するのである。この点で,4次元は,他のどの領域よりも無限に奇妙な場所である.他のすべての次元nに対して,Rnのバージョンは1つしか存在しない.結局のところ、4次元は、SF作家の想像する奇妙な世界の数学的設定に適しているのだろう。
ドデカプレックスと呼ばれる4次元の物体を含む投影です。画像はPaul Nylanderが作成しました。
著者について
Richard Elwesはリーズ大学の客員研究員である。2006年にPlus New Writers Awardを受賞して以来、New ScientistやDaily Telegraphに記事を掲載し、公の場やラジオで定期的に数学について話しています。著書に『Plus』で紹介した『Maths 1001』、『How to build a brain and 34 other really interesting uses of mathematics』(2011年3月)がある。
DeepL翻訳




0 件のコメント:
コメントを投稿